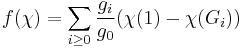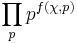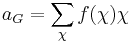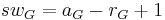Artin conductor
In mathematics, the Artin conductor is a number or ideal associated to a character of a Galois group of a local or global field, introduced by Artin (1930, 1931) as an expression appearing in the functional equation of an Artin L-function.
Contents |
Local Artin conductors
Suppose that L is a finite Galois extension of the local field K, with Galois group G. If χ is a character of G, then the Artin conductor of χ is the number
where Gi is the ith ramification group, of order gi, and χ(Gi) is the average value of χ on Gi.
Global Artin conductors
The global Artin conductor is an ideal associated to a representation χ of the Galois group G of a finite extension L/K of global fields. It is defined to be
where the product is over the primes p of K, and f(χ,p) is the local Artin conductor of the restriction of χ to the decomposition group of some prime of L lying over p.
Artin representation and Artin character
Suppose that L is a finite Galois extension of the local field K, with Galois group G. The Artin character aG of G is the character
and the Artin representation AG is the complex linear representation of G with this character. Weil (1946) asked for a direct construction of the Artin representation. Serre (1960) showed that the Artin representation can be realized over the local field Ql, for any prime l not equal to the residue characteristic p. Fontaine (1971) showed that it can be realized over the corresponding ring of Witt vectors. It cannot in general be realized over the rationals or over the local field Qp, suggesting that there is no easy way to construct the Artin representation explicitly.
Swan representation
The Swan character swG is given by
where rg is the character of the regular representation and 1 is the character of the trivial representation. The Swan character is the character of a representation of G. Swan (1963) showed that there is a unique projective representation of G over the l-adic integers with character the Swan character.
Applications
The Artin conductor appears in the conductor-discriminant formula for the discriminant of a global field.
The optimal level in the Serre modularity conjecture is expressed in terms of the Artin conductor.
The Artin conductor appears in the functional equation of the Artin L-function.
References
- Artin, Emil (1930), "Zur Theorie der L-Reihen mit allgemeinen Gruppencharakteren." (in German), Abhandlungen Hamburg 8: 292–306, doi:10.1007/BF02941010, JFM 56.0173.02
- Artin, Emil (1931), "Die gruppentheoretische Struktur der Diskriminanten algebraischer Zahlkörper." (in German), Journal für Reine und Angewandte Mathematik 164: 1–11, doi:10.1515/crll.1931.164.1, ISSN 0075-4102, Zbl 0001.00801, http://resolver.sub.uni-goettingen.de/purl?GDZPPN002171422
- Fontaine, Jean-Marc (1971), "Sur les représentations d'Artin", Colloque de Théorie des Nombres (Univ. Bordeaux, Bordeaux, 1969), Mémoires de la Société Mathématique de France, 25, Paris: Société Mathématique de France, pp. 71–81, MR0374106, http://www.numdam.org/item?id=MSMF_1971__25__71_0
- Serre, Jean-Pierre (1960), "Sur la rationalité des représentations d'Artin", Annals of Mathematics. Second Series 72: 405–420, ISSN 0003-486X, MR0171775, http://www.jstor.org/stable/1970142
- Swan, Richard G. (1963), "The Grothendieck ring of a finite group", Topology. An International Journal of Mathematics 2: 85–110, doi:10.1016/0040-9383(63)90025-9, ISSN 0040-9383, MR0153722
- Weil, André (1946), "L'avenir des mathématiques", Bol. Soc. Mat. São Paulo 1: 55–68, MR0020961